这部分主要代码在函数FullSystem::trackNewCoarse中。首先,DSO设置了一系列的候选位姿lastF_2_fh_tries,作为前一关键帧到当前帧的相对位姿的初值。这里主要参考前两帧和前一关键帧的位姿,就静止、恒定速度等猜想设了一些初值,另外主要针对旋转设置了许多微小的初始值。然后开始不断地尝试,从图像金字塔顶层开始就这些初值进行追踪CoarseTracker::trackNewestCoarse,如果找到一个合适的初值,就跳出循环。先来看一下追踪部分是如何实现的。函数CoarseTracker::trackNewestCoarse,传入参数有当前帧newFrameHessian,预测的相对位姿lastToNew_out,预测的相对光度aff_g2l_out(初始化为0),金字塔层数coarsestLvl,用来判断是否合适的误差minResForAbort,返回一个表明是否成功的bool值。该函数从输入的金字塔层级开始,由粗到精地计算最佳位姿。
先是计算当前误差的大小CoarseTracker::calcRes。这一步里还没有改变位姿的大小,仅仅将host帧(参考帧,前一关键帧)的点, 通过反投影变换 以及投影变换 变换到Target帧(最新帧)的图像平面,然后将误差累计起来返回,并保存了后续计算雅克比矩阵需要的变量。这里和初始化时不同的是,追踪时已经有了一定的点,因此只考虑位姿加光度共8个参数。
将host帧上的点x 1 x_1 x 1
X 1 = ρ 1 − 1 K − 1 x 1 x 2 = K ρ 2 ( R 21 ρ 1 − 1 K − 1 x 1 + t 21 ) = K x 2 ′ \begin{aligned} X_{1} &=\rho_{1}^{-1} K^{-1} x_{1} \\ x_{2} &=K \rho_{2}\left(R_{21} \rho_{1}^{-1} K^{-1} x_{1}+t_{21}\right) \\ &=K x_{2}^{\prime} \end{aligned} X 1 x 2 = ρ 1 − 1 K − 1 x 1 = K ρ 2 ( R 2 1 ρ 1 − 1 K − 1 x 1 + t 2 1 ) = K x 2 ′
上式中的 x 2 ′ x_2^{\prime} x 2 ′ x 2 ′ = [ u 2 ′ , v 2 ′ , 1 ] T x_{2}^{\prime}=\left[u_{2}^{\prime}, v_{2}^{\prime}, 1\right]^{T} x 2 ′ = [ u 2 ′ , v 2 ′ , 1 ] T
设误差函数 r 21 = ( I 2 ( p 2 ) − b 2 ) − ( e x p ( a 21 ) I 1 ( p 1 ) − b 1 ) r_{21}=(I_{2}\left(\mathbf{p}_{2}\right)-b_2)-\left(exp (a_{21})I_{1}(\mathbf{p}_{1}\right)-b_{1}) r 2 1 = ( I 2 ( p 2 ) − b 2 ) − ( e x p ( a 2 1 ) I 1 ( p 1 ) − b 1 )
对相对光度参数求导 :
∂ r 21 ∂ a 21 = − exp ( a 21 ) I 1 ( p 1 ) \frac{\partial r_{21}}{\partial a_{21}}=-\exp (a_{21})I_{1}\left(\mathbf{p}_{1}\right) ∂ a 2 1 ∂ r 2 1 = − exp ( a 2 1 ) I 1 ( p 1 ) ∂ r 21 ∂ b 21 = − 1 \frac{\partial r_{21}}{\partial b_{21}}=-1 ∂ b 2 1 ∂ r 2 1 = − 1
对位姿增量求导
∂ r 21 ∂ ξ 21 = ∂ r 21 ∂ x 2 ∂ x 2 ∂ ξ 21 \frac{\partial r_{21}}{\partial \xi_{21}}=\frac{\partial r_{21}}{\partial x_{2}} \frac{\partial x_{2}}{\partial \xi_{21}} ∂ ξ 2 1 ∂ r 2 1 = ∂ x 2 ∂ r 2 1 ∂ ξ 2 1 ∂ x 2
其中,∂ r 21 ∂ x 2 = ∂ I 2 [ x 2 ] ∂ x 2 = [ d x d y ] \frac{\partial r_{21}}{\partial x_{2}}= \frac{\partial I_{2}\left[x_{2}\right]}{\partial x_{2}}=\left[\begin{array}{l}d_{x} \\ d_{y}\end{array}\right] ∂ x 2 ∂ r 2 1 = ∂ x 2 ∂ I 2 [ x 2 ] = [ d x d y ]
通过链式法则
∂ x 2 ∂ ξ 21 = ∂ x 2 ∂ x 2 ′ ∂ x 2 ′ ∂ ξ 21 \frac{\partial x_{2}}{\partial \xi_{21}}=\frac{\partial x_{2}}{\partial x_{2}^{\prime}} \frac{\partial x_{2}^{\prime}}{\partial \xi_{21}} ∂ ξ 2 1 ∂ x 2 = ∂ x 2 ′ ∂ x 2 ∂ ξ 2 1 ∂ x 2 ′
∂ x 2 ∂ x 2 ′ = [ f x 0 0 0 f y 0 0 0 0 ] \begin{aligned} \frac{\partial x_{2}}{\partial x_{2}^{\prime}} &=\left[\begin{array}{ccc}f_{x} & 0 & 0 \\ 0 & f_{y} & 0 \\ 0 & 0 & 0\end{array}\right] \end{aligned} ∂ x 2 ′ ∂ x 2 = ⎣ ⎡ f x 0 0 0 f y 0 0 0 0 ⎦ ⎤
x 2 ′ = ρ 2 ( R 21 X 1 + t 21 ) = ρ 2 X 2 x_{2}^{\prime}=\rho_{2}\left(R_{21} X_{1}+t_{21}\right)=\rho_{2} X_{2} x 2 ′ = ρ 2 ( R 2 1 X 1 + t 2 1 ) = ρ 2 X 2 ρ 2 \rho_2 ρ 2
∂ X 2 ∂ ξ 21 = [ ∂ X 2 ∂ ξ 21 ∂ Y 2 ∂ ξ 21 ∂ Z 2 ∂ ξ 21 ] = [ 1 0 0 0 Z 2 − Y 2 0 1 0 − Z 2 0 X 2 0 0 1 Y 2 − X 2 0 ] ∂ x 2 ′ ∂ ξ 21 = [ ∂ ρ 2 ∂ ξ 21 X 2 ∂ ρ 2 ∂ ξ 21 Y 2 ∂ ρ 2 ∂ ξ 21 Z 2 ] + ρ 2 ∂ X 2 ∂ ξ 21 \begin{aligned} \frac{\partial X_{2}}{\partial \xi_{21}} &=\left[\begin{array}{lllll}\frac{\partial X_{2}}{\partial \xi_{21}} \\ \frac{\partial Y_{2}}{\partial \xi_{21}} \\ \frac{\partial Z_{2}}{\partial \xi_{21}}\end{array}\right] \\ &=\left[\begin{array}{llll}1 & 0 & 0 & 0 & Z_{2} & -Y_{2} \\ 0 & 1 & 0 & -Z_{2} & 0 & X_{2} \\ 0 & 0 & 1 & Y_{2} & -X_{2} & 0\end{array}\right] \\ & \frac{\partial x_{2}^{\prime}}{\partial \xi_{21}}=\left[\begin{array}{cc}\frac{\partial \rho_{2}}{\partial \xi_{21}} X_{2} \\ \frac{\partial \rho_{2}}{\partial \xi_{21}} Y_{2} \\ \frac{\partial \rho_{2}}{\partial \xi_{21}} Z_{2}\end{array}\right]+\rho_{2} \frac{\partial X_{2}}{\partial \xi_{21}} \end{aligned} ∂ ξ 2 1 ∂ X 2 = ⎣ ⎢ ⎡ ∂ ξ 2 1 ∂ X 2 ∂ ξ 2 1 ∂ Y 2 ∂ ξ 2 1 ∂ Z 2 ⎦ ⎥ ⎤ = ⎣ ⎡ 1 0 0 0 1 0 0 0 1 0 − Z 2 Y 2 Z 2 0 − X 2 − Y 2 X 2 0 ⎦ ⎤ ∂ ξ 2 1 ∂ x 2 ′ = ⎣ ⎢ ⎡ ∂ ξ 2 1 ∂ ρ 2 X 2 ∂ ξ 2 1 ∂ ρ 2 Y 2 ∂ ξ 2 1 ∂ ρ 2 Z 2 ⎦ ⎥ ⎤ + ρ 2 ∂ ξ 2 1 ∂ X 2
最终可得:
∂ r 21 ∂ δ ξ 21 = [ d x , d y , 0 ] [ f x ρ 2 0 − f x ρ 2 u 2 ′ − f x u 2 ′ v 2 ′ f x ( 1 + u 2 ′ 2 ) − f x v 2 ′ 0 f y ρ 2 − f y ρ 2 v 2 ′ − f y ( 1 + v 2 ′ 2 ) f y u 2 ′ v 2 ′ f y u 2 ′ 0 0 0 0 0 0 ] \frac{\partial r_{21}}{\partial \delta \xi_{21}}=[d_x,d_y,0]\left[\begin{array}{cccccc}f_{x} \rho_{2} & 0 & -f_{x} \rho_{2} u_{2}^{\prime} & -f_{x} u_{2}^{\prime} v_{2}^{\prime} & f_{x}\left(1+u_{2}^{\prime 2}\right) & -f_{x} v_{2}^{\prime} \\ 0 & f_{y} \rho_{2} & -f_{y} \rho_{2} v_{2}^{\prime} & -f_{y}\left(1+v_{2}^{\prime 2}\right) & f_{y} u_{2}^{\prime} v_{2}^{\prime} & f_{y} u_{2}^{\prime} \\ 0 & 0 & 0 & 0 & 0 & 0\end{array}\right] ∂ δ ξ 2 1 ∂ r 2 1 = [ d x , d y , 0 ] ⎣ ⎡ f x ρ 2 0 0 0 f y ρ 2 0 − f x ρ 2 u 2 ′ − f y ρ 2 v 2 ′ 0 − f x u 2 ′ v 2 ′ − f y ( 1 + v 2 ′ 2 ) 0 f x ( 1 + u 2 ′ 2 ) f y u 2 ′ v 2 ′ 0 − f x v 2 ′ f y u 2 ′ 0 ⎦ ⎤
逆深度的雅可比
∂ r 21 ∂ ρ 1 = ∂ r 21 ∂ x 2 ∂ x 2 ∂ ρ 1 = ∂ I 2 [ x 2 ] ∂ x 2 ∂ x 2 ∂ ρ 1 = [ d x d y 0 ] [ f x ρ 1 − 1 ρ 2 ( t 21 x − u 2 ′ t 21 z ) f y ρ 1 − 1 ρ 2 ( t 21 y − v 2 ′ t 21 z ) ] = ( d x f x ρ 1 − 1 ρ 2 ( t 21 x − u 2 ′ t 21 z ) + d y f y ρ 1 − 1 ρ 2 ( t 21 y − v 2 ′ t 21 z ) ) \begin{aligned} \frac{\partial r_{21}}{\partial \rho_{1}} &=\frac{\partial r_{21}}{\partial x_{2}} \frac{\partial x_{2}}{\partial \rho_{1}} \\ &=\frac{\partial I_{2}\left[x_{2}\right]}{\partial x_{2}} \frac{\partial x_{2}}{\partial \rho_{1}} \\ &=\left[d_{x} \quad d_{y} \quad 0\right]\left[\begin{array}{cc}f_{x} \rho_{1}^{-1} \rho_{2}\left(t_{21}^{x}-u_{2}^{\prime} t_{21}^{z}\right) \\ f_{y} \rho_{1}^{-1} \rho_{2}\left(t_{21}^{y}-v_{2}^{\prime} t_{21}^{z}\right)\end{array}\right] \\ &=\left(d_{x} f_{x} \rho_{1}^{-1} \rho_{2}\left(t_{21}^{x}-u_{2}^{\prime} t_{21}^{z}\right)+d_{y} f_{y} \rho_{1}^{-1} \rho_{2}\left(t_{21}^{y}-v_{2}^{\prime} t_{21}^{z}\right)\right) \end{aligned} ∂ ρ 1 ∂ r 2 1 = ∂ x 2 ∂ r 2 1 ∂ ρ 1 ∂ x 2 = ∂ x 2 ∂ I 2 [ x 2 ] ∂ ρ 1 ∂ x 2 = [ d x d y 0 ] [ f x ρ 1 − 1 ρ 2 ( t 2 1 x − u 2 ′ t 2 1 z ) f y ρ 1 − 1 ρ 2 ( t 2 1 y − v 2 ′ t 2 1 z ) ] = ( d x f x ρ 1 − 1 ρ 2 ( t 2 1 x − u 2 ′ t 2 1 z ) + d y f y ρ 1 − 1 ρ 2 ( t 2 1 y − v 2 ′ t 2 1 z ) )
接下来在函数CoarseTracker::calcGSSSE中计算增量方程中的H和b。上一节已经求得了对应变量的导数,它们在代码中的表示为
1 2 3 4 5 6 7 8 9 10 11 12 13 14 _mm_mul_ps(id,dx), _mm_mul_ps(id,dy), _mm_sub_ps(zero, _mm_mul_ps(id,_mm_add_ps(_mm_mul_ps(u,dx), _mm_mul_ps(v,dy)))), _mm_sub_ps(zero, _mm_add_ps( _mm_mul_ps(_mm_mul_ps(u,v),dx), _mm_mul_ps(dy,_mm_add_ps(one, _mm_mul_ps(v,v))))), _mm_add_ps( _mm_mul_ps(_mm_mul_ps(u,v),dy), _mm_mul_ps(dx,_mm_add_ps(one, _mm_mul_ps(u,u)))), _mm_sub_ps(_mm_mul_ps(u,dy), _mm_mul_ps(v,dx)), _mm_mul_ps(a,_mm_sub_ps(b0, _mm_load_ps(buf_warped_refColor+i))), minusOne, _mm_load_ps(buf_warped_residual+i), _mm_load_ps(buf_warped_weight+i));
可以得到: H = J T W J \mathbf{H}=\mathbf{J}^{T} \mathbf{W} \mathbf{J} H = J T W J
初始的lambda设为0.01(即列文伯格方法中的拉格让日乘子λ\lambdaλ),然后求解增量方程( H + λ I ) Δ x = b (\mathbf{H}+\lambda \mathbf{I}) \Delta \mathbf{x}=\mathbf{b} ( H + λ I ) Δ x = b
得到增量后对原来的状态变量进行更新x ← x + Δ x \mathbf{x} \leftarrow \mathbf{x}+\Delta \mathbf{x} x ← x + Δ x
每一层的最大迭代次数是固定的,且各不相同,高层的次数多,低层的次数少
初始的lambda设为0.01(即列文伯格方法中的拉格让日乘子λ\lambdaλ),然后求解增量方程
得到增量后对原来的状态变量进行更新
注意位姿的更新不是李代数相加,而是指数映射到李群后相乘
1 2 3 4 SE3 refToNew_new = SE3::exp((Vec6)(incScaled.head<6>())) * refToNew_current; AffLight aff_g2l_new = aff_g2l_current; aff_g2l_new.a += incScaled[6]; aff_g2l_new.b += incScaled[7];
用新的状态变量重新计算误差,然后将新的误差和旧的误差做比较,考虑是否接受这次优化
bool accept = (resNew[0] / resNew[1]) < (resOld[0] / resOld[1]);
这里的resNew[0]是总的误差,resNew[1]是对应点的数量,当平均误差减小时,认为这次优化可以接受。如果可以接受,那么就缩小lambda(每次缩小为原来的二分之一),如果优化失败,那么就说明高斯牛顿法的二次函数近似效果在这里不太好,通过增大lambda(放大为原来的4倍)来改善。当某一次得到的增量小于一定值时,认为收敛了,迭代过程终止。
关键帧的选择主要考虑当前帧和前一关键帧(参考帧)在点的光流变化,不考虑旋转情况下的光流变化,曝光参数的变化,三者加权相加大于1时新建关键帧
如果当前帧被认为是非关键帧,那么该帧就用来对活动窗口中所有的关键帧中还未成熟的点进行逆深度更新: traceNewCoarse(fh);(深度滤波)
基本原理是沿着极线进行搜索ImmaturePoint::traceOn
首先,将未成熟的点根据相对位姿和之前的逆深度投影到当前帧上
1 2 3 4 Vec3f pr = hostToFrame_KRKi * Vec3f(u,v, 1); Vec3f ptpMin = pr + hostToFrame_Kt*idepth_min; float uMin = ptpMin[0] / ptpMin[2]; float vMin = ptpMin[1] / ptpMin[2];
这里的(uMin,vMin)就是设逆深度最小时投影得到的像素坐标。
接下来确定极线,如果逆深度无限大,随便设一个逆深度0.01,得到另一个投影点的坐标(uMax,vMax),
1 2 3 4 // project to arbitrary depth to get direction. ptpMax = pr + hostToFrame_Kt*0.01; uMax = ptpMax[0] / ptpMax[2]; vMax = ptpMax[1] / ptpMax[2];
这样就得到了极线的方向
1 2 3 4 // direction. float dx = uMax-uMin; float dy = vMax-vMin; float d = 1.0f / sqrtf(dx*dx+dy*dy);
这样,极线可以表示为L : = { l 0 + λ [ l x , l y ] T } \mathbf{L}:=\left\{\mathbf{l}_{0}+\lambda\left[l_{x}, l_{y}\right]^{T}\right\} L : = { l 0 + λ [ l x , l y ] T }
其中l 0 l_0 l 0 [ u m i n , v m i n ] T [\ { u_{min} }, \ v_{min }]^{T} [ u m i n , v m i n ] T [ l x , l y ] T \left[l_{x}, l_{y}\right]^{T} [ l x , l y ] T
1 2 3 dist = maxPixSearch; uMax = uMin + dist*dx*d; vMax = vMin + dist*dy*d;
然后在最大范围内按一定步长进行离散搜索,找到最小的和第二小的误差,比较两者的比值。最后在最小误差的位置上进行高斯牛顿优化(只有一个变量),每次迭代过程中如果误差大于前面得到的最小误差,就缩小优化步长重新来过,当增量小于一定值时停止。
设P r = K R K − 1 [ u 1 v 1 1 ] T = [ m 1 m 2 m 3 ] T \mathbf{P}_{r}=\mathbf{K R K}^{-1}\left[\begin{array}{lll}u_{1} & v_{1} & 1\end{array}\right]^{T}=\left[\begin{array}{lll}m_{1} & m_{2} & m_{3}\end{array}\right]^{T} P r = K R K − 1 [ u 1 v 1 1 ] T = [ m 1 m 2 m 3 ] T K t = [ n 1 n 2 n 3 ] T \mathbf{K t}=\left[\begin{array}{lll}n_{1} & n_{2} & n_{3}\end{array}\right]^{T} K t = [ n 1 n 2 n 3 ] T
则投影后的像素坐标
$u_{2}=\frac{m_{1}+n_{1} \rho_{1}}{m_{3}+n_{3} \rho_{1}} $$v_{2}=\frac{m_{2}+n_{2} \rho_{1}}{m_{3}+n_{3} \rho_{1}}$
把逆深度放在左边,$\rho_{1}=\frac{m_{3} u_{2}-m_{1}}{n_{1}-n_{3} u_{2}} $ (1) $ \rho_{1}=\frac{m_{3} v_{2}-m_{2}}{n_{2}-n_{3} v_{2}}$ (2)
设[ u 2 ∗ , v 2 ∗ ] T \left[u_{2}^{*}, v_{2}^{*}\right]^{T} [ u 2 ∗ , v 2 ∗ ] T ρ 1 min = m 3 ( u 2 ∗ − α Δ u ) − m 1 n 1 − n 3 ( u 2 ∗ − α Δ u ) \rho_{1 \min }=\frac{m_{3}\left(u_{2}^{*}-\alpha \Delta u\right)-m_{1}}{n_{1}-n_{3}\left(u_{2}^{*}-\alpha \Delta u\right)} ρ 1 min = n 1 − n 3 ( u 2 ∗ − α Δ u ) m 3 ( u 2 ∗ − α Δ u ) − m 1 ρ 1 max = m 3 ( u 2 ∗ + α Δ u ) − m 1 n 1 − n 3 ( u 2 ∗ + α Δ u ) \rho_{1 \max }=\frac{m_{3}\left(u_{2}^{*}+\alpha \Delta u\right)-m_{1}}{n_{1}-n_{3}\left(u_{2}^{*}+\alpha \Delta u\right)} ρ 1 max = n 1 − n 3 ( u 2 ∗ + α Δ u ) m 3 ( u 2 ∗ + α Δ u ) − m 1
当y方向梯度较大时,根据公式(2)来确定逆深度范围:
ρ 1 min = m 3 ( v 2 ∗ − α Δ v ) − m 2 n 2 − n 3 ( v 2 ∗ − α Δ v ) \rho_{1 \min }=\frac{m_{3}\left(v_{2}^{*}-\alpha \Delta v\right)-m_{2}}{n_{2}-n_{3}\left(v_{2}^{*}-\alpha \Delta v\right)} ρ 1 min = n 2 − n 3 ( v 2 ∗ − α Δ v ) m 3 ( v 2 ∗ − α Δ v ) − m 2 ρ 1 max = m 3 ( v 2 ∗ + α Δ v ) − m 2 n 2 − n 3 ( v 2 ∗ + α Δ v ) \rho_{1 \max }=\frac{m_{3}\left(v_{2}^{*}+\alpha \Delta v\right)-m_{2}}{n_{2}-n_{3}\left(v_{2}^{*}+\alpha \Delta v\right)} ρ 1 max = n 2 − n 3 ( v 2 ∗ + α Δ v ) m 3 ( v 2 ∗ + α Δ v ) − m 2
1 2 3 4 5 6 7 8 9 10 if (dx*dx>dy*dy){ idepth_min = (pr[2 ]*(bestU-errorInPixel*dx) - pr[0 ]) / (hostToFrame_Kt[0 ] - hostToFrame_Kt[2 ]*(bestU-errorInPixel*dx)); idepth_max = (pr[2 ]*(bestU+errorInPixel*dx) - pr[0 ]) / (hostToFrame_Kt[0 ] - hostToFrame_Kt[2 ]*(bestU+errorInPixel*dx)); } else { idepth_min = (pr[2 ]*(bestV-errorInPixel*dy) - pr[1 ]) / (hostToFrame_Kt[1 ] - hostToFrame_Kt[2 ]*(bestV-errorInPixel*dy)); idepth_max = (pr[2 ]*(bestV+errorInPixel*dy) - pr[1 ]) / (hostToFrame_Kt[1 ] - hostToFrame_Kt[2 ]*(bestV+errorInPixel*dy)); }
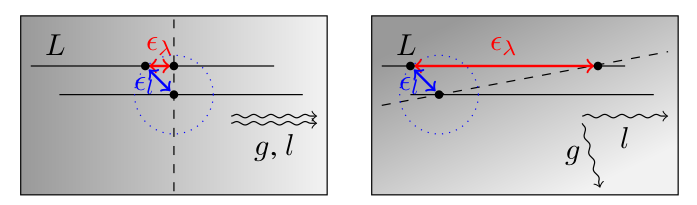
接下来考虑α。为什么这里要有个α呢?前面通过离散搜索加上高斯牛顿优化的方式得到了最佳的匹配点,如果假设没有其他任何误差存在的话,我们完全可以令α=1,这样逆深度的最大最小值就可以通过简单地扰动一个单位步长来得到。但考虑误差的话,我们会发现极线和梯度的夹角对结果有着非常大的影响。如果极线的方向和梯度的方向接近垂直的,那么稍微有一点位姿误差(必然存在)使得投影点和真实点产生了一定的误差,沿着极线搜索得到的结果就会产生巨大的偏差,如图1所示。因此,非常有必要考虑这个α,事实上,在代码中,α的计算是在极线搜索之前做的,如果得到的α太大(这意味这极线和梯度的夹角接近90度),就没有做极线搜索的必要。
DSO似乎没有直接根据公式计算视差的不确定度,α更像是一个根据人工经验设计的置信系数(我目前是这么理解的,因为实在推不出这个公式),代码如下所示:
1 2 3 4 5 6 float dx = setting_trace_stepsize*(uMax-uMin); float dy = setting_trace_stepsize*(vMax-vMin); float a = (Vec2f(dx,dy).transpose() * gradH * Vec2f(dx,dy)); float b = (Vec2f(dy,-dx).transpose() * gradH * Vec2f(dy,-dx)); float errorInPixel = 0.2f + 0.2f * (a+b) / a;
令点在主导帧中的梯度雅克比为J ∇ = [ ∇ x , ∇ y ] T \mathbf{J}_{\nabla}=[\nabla x, \nabla y]^{T} J ∇ = [ ∇ x , ∇ y ] T ∑ J ∇ J ∇ T \sum \mathbf{J}_{\nabla} \mathbf{J}_{\nabla}^{T} ∑ J ∇ J ∇ T